Integrasjon
Contents
Integrasjon#
Det er fleire måtar me kan approksimera bestemte integral numerisk. I GeoGebra finn me funksjonane “SumUnder” og “SumOver” som gjev oss summen av arealet til \(n\) rektangel mellom \(a\) og \(b\) på \(x\)-aksen som er slik at dei ligg under eller over funksjonen. “SumUnder” vil dermed gje eit resultat som er litt mindre enn det faktiske resultatet, medan “SumOver” vil gje eit litt for stort resultat.
Animasjonen under viser korleis nøyaktigheita aukar etter kvart som antall rektangel vert større. Med fleire rektangel vert arealet som ikkje vert dekka mindre og mindre.
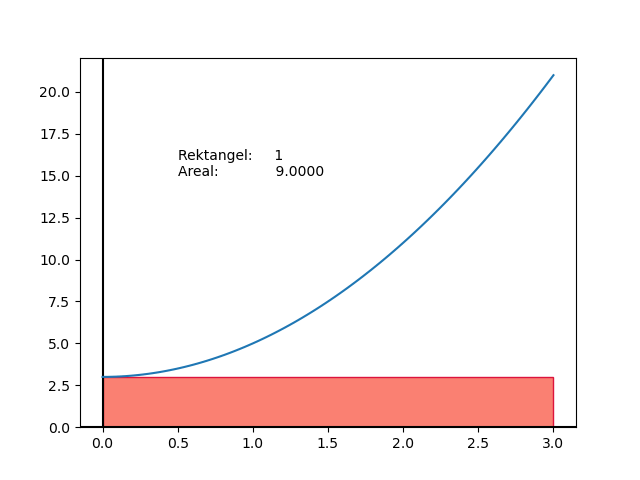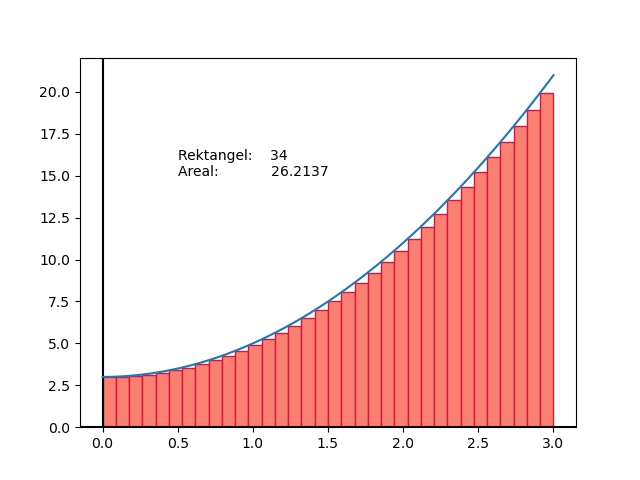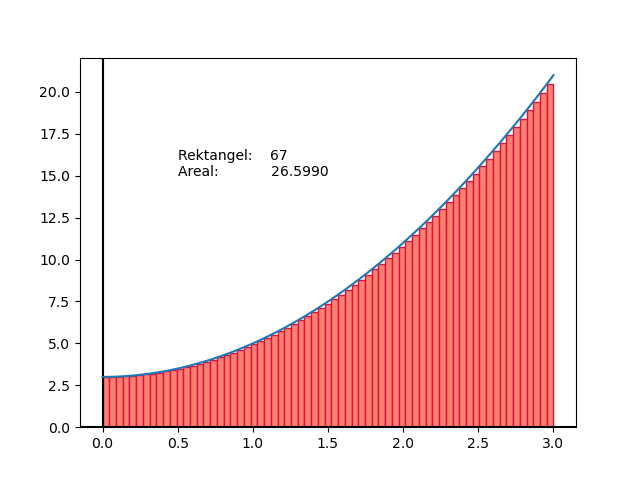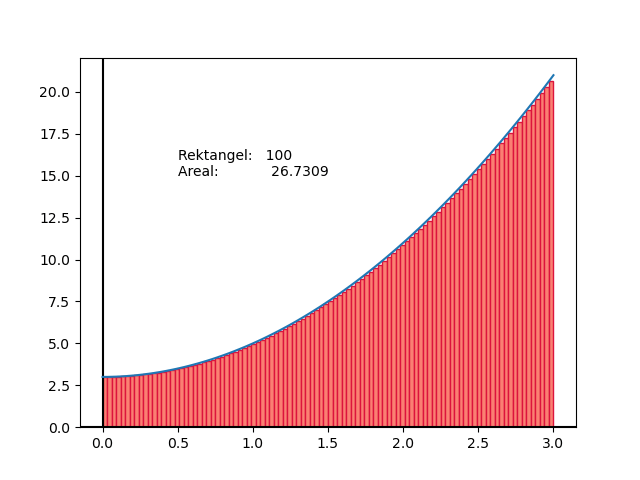
Fig. 1 Samanheng mellom nøyaktigheit og tal rektangel.#
Den enklaste approksimasjonen er å finna venstre- eller høgresum. Med venstresum skal kvar av rektangla ha høgde slik at hjørnet øverst til venstre ligg på funksjonen. Høgresum finn me på same måte, men med hjørnet øverst til høgre på funksjonen. Algoritmen vert ganske lik for begge. Me ser på venstresum først.
Venstresum#
Me skal finna summen av \(n\) rektangel mellom \(a\) og \(b\) som er slik at hjørnet øverst til venstre på kvart rektangel ligg på funksjonen. Breidda til rektangla kallar me dx.
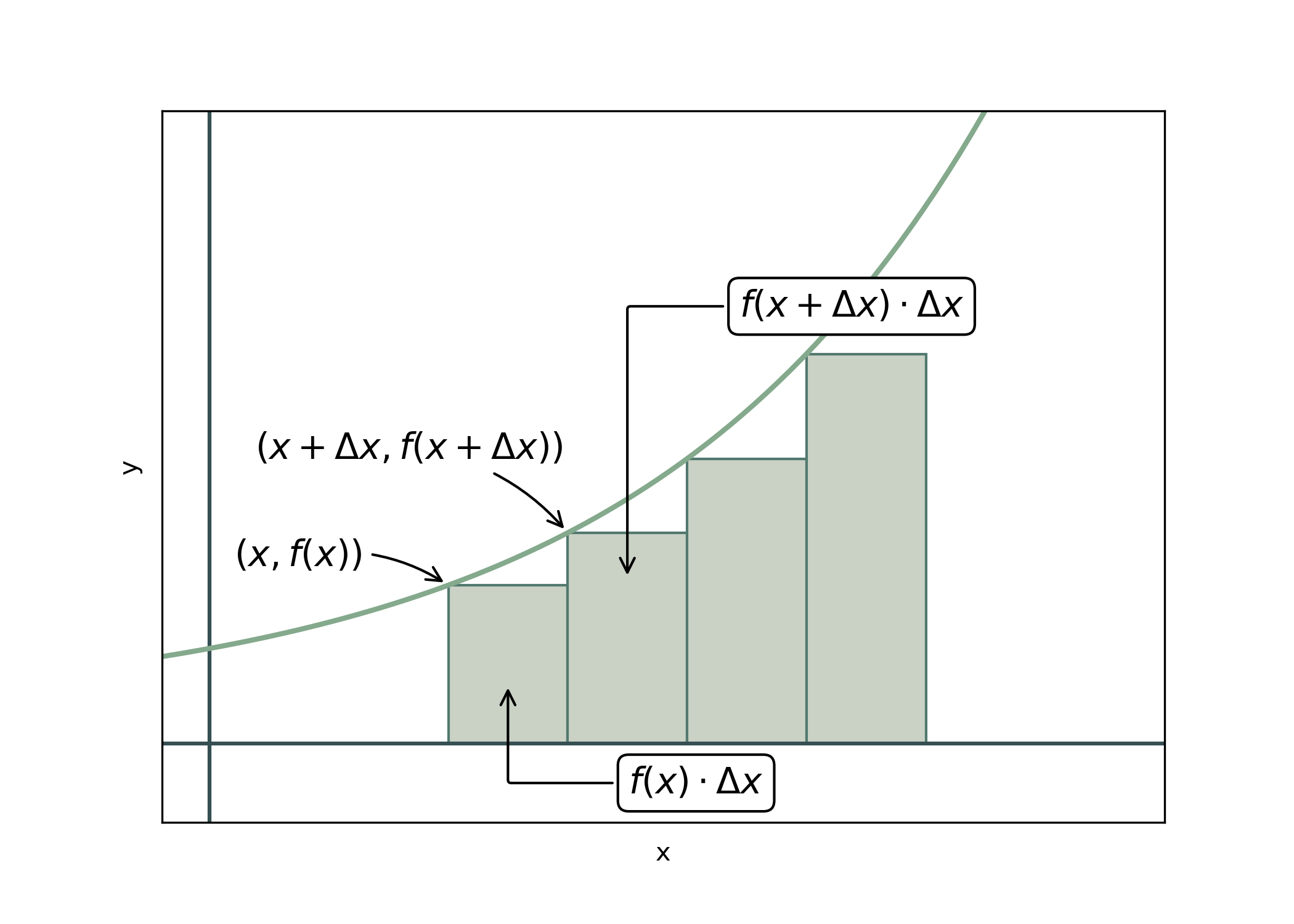
Fig. 2 Samanheng mellom rektangel og funksjon.#
def venstresum(f, a, b, n):
dx = (b-a)/n
x = a
sum_venstre = 0
for i in range(n):
rektangel = f(x)*dx
sum_venstre += rektangel
x += dx
return sum_venstre
Tester på funksjonen
Leiter etter ein omtrentleg verdi av arealet under \(f(x)\) frå \(x=2\) til \(x=5\).
def f(x):
return x**3 + 2*x + 3
print(f"Venstresum: {venstresum(f, 2, 5, 100):.3f}")
Venstresum: 180.410
Høgresum#
Me skal finna summen av \(n\) rektangel mellom \(a\) og \(b\) som er slik at hjørnet øverst til høgre på kvart rektangel ligg på funksjonen.
Breidda til rektangla kallar me dx. Funksjonen er heilt lik som i venstresum() men me endrar rektangel til f(x+dx)*dx slik at me reknar høgda på høgresida av rektangelet.
def høgresum(f, a, b, n):
dx = (b-a)/n
x = a
sum_høgre = 0
for i in range(n):
rektangel = f(x+dx)*dx
sum_høgre += rektangel
x += dx
return sum_høgre
Testar med same funksjon og intervall som tidlegare.
print(f"Høgresum: {høgresum(f, 2, 5, 100):.3f}")
Høgresum: 184.100
Med det kan me anta at
Bruker me fleire rektangel, vil me få ein betre approksimasjon:
print(f"Venstresum: {venstresum(f, 2, 5, 1000):.3f}")
print(f"Høgresum: {høgresum(f, 2, 5, 1000):.3f}")
Venstresum: 182.066
Høgresum: 182.435
Sum under og sum over#
Viss me vil finna tilsvarande GeoGebra sin SumUnder må me sjekka kva side av kvart rektangel som er kortast, for så å bruka det som høgde.
def sumunder(f, a, b, n):
dx = (b-a)/n
x = a
sum_under = 0
for i in range(n):
if f(x) <= f(x+dx):
rektangel = f(x)*dx
else:
rektangel = f(x+dx)*dx
sum_under += rektangel
x += dx
return sum_under
Sum over blir heilt analogt, men me snur ulikskapen i viss-setningen:
def sumover(f, a, b, n):
dx = (b-a)/n
x = a
sum_over = 0
for i in range(n):
if f(x) >= f(x+dx):
rektangel = f(x)*dx
else:
rektangel = f(x+dx)*dx
sum_over += rektangel
x += dx
return sum_over
print(f"Sum under: {sumunder(f, 2, 5, 100):.3f}")
print(f"Sum over: {sumover(f, 2, 5, 100):.3f}")
Sum under: 180.410
Sum over: 184.100
Trapesmetoden#
Ein enno betre approksimasjon er å laga trapes framfor rektangel. Høgda på trapeset vert dx medan dei to parallelle sidene vert f(x) og f(x+dx).
def trapesmetoden(f, a, b, n):
dx = (b-a)/n
x = a
sum_trapes = 0
for i in range(n):
trapes = ((f(x)+f(x+dx))*dx)/2
sum_trapes += trapes
x += dx
return sum_trapes
print(f"Trapesmetode: {trapesmetoden(f, 2, 5, 100):.3f}")
Trapesmetode: 182.255
Reknar me ut integralet vil me sjå at svaret vert
Med trapesmetoden kjem me altså nærare svaret med 100 trapes enn med venstresum med 1000 rektangel.

