Terningar
Contents
Terningar#
Obs!
Eg nyttar den anbefalte måten å nytta numpy.random (sjekk dokumentasjonen)
import numpy as np # Importerer numpy som np
from numpy.random import default_rng # Importerer default_rng
rng = default_rng() # Lager en rng (random number generator)
Ein og ein terning#
Det enklaste dømet på simulering av stokastiske forsøk er trilling av terning
terning = rng.integers(1, 7)
print(terning)
4
Viss me vil kan me bruka løkker for å trilla terningar fleire gongar:
for i in range(10):
print(rng.integers(1, 7))
1
6
2
6
3
1
5
3
4
6
eller så kan me legga inn ein verdi for size i funksjonen. Dette vil gje oss ein array med size terningar.
terningar = rng.integers(1, 7, size=10)
print(terningar)
[6 3 2 6 5 2 2 5 2 1]
Viss me til dømes vil finna ut kor sannsynleg det er å trilla 5 eller 6 gjennom simulering så kan me gjera det på ulike måtar. Basert på dei to alternativa over gjer det oss desse to:
Alternativ 1 - løkke#
N = 1000000
gunstige = 0
for i in range(N):
terning = rng.integers(1, 7)
if terning >= 5:
gunstige += 1
sannsyn = gunstige / N
print(f"Sannsynet for å trilla 5 eller høgare er {round(sannsyn, 3)}")
Sannsynet for å trilla 5 eller høgare er 0.333
Alternativ 2 - array#
N = 1000000
terningar = rng.integers(1, 7, size=N)
gunstige = sum(terningar >= 5) # finn antall terningar som er større eller lik 5
sannsyn = gunstige / N
print(f"Sannsynet for å trilla 5 eller høgare er {round(sannsyn, 3)}")
Sannsynet for å trilla 5 eller høgare er 0.333
Fleire terningar#
Spørsmål som “Kva er sannsynet for at produktet av to terningar er 8 eller mindre” er fint å finna svar på ved hjelp av simulering. Igjen kan me gjera det på fleire måtar, eg viser ved hjelp av løkker og arrays.
Alternativ 1 - løkke#
N = 1000000
gunstige = 0
for i in range(N):
terning1 = rng.integers(1, 7)
terning2 = rng.integers(1, 7)
# sjekkar om produktet er 8 eller mindre
if terning1 * terning2 <= 8:
gunstige += 1
sannsyn = gunstige / N
print(f"Sannsynet for at produktet av to terningar er 8 eller mindre er {round(sannsyn, 3)}")
Sannsynet for at produktet av to terningar er 8 eller mindre er 0.444
Alternativ 2 - arrays#
N = 1000000
terning1 = rng.integers(1, 7, size = N)
terning2 = rng.integers(1, 7, size = N)
produkt = terning1 * terning2
gunstige = sum(produkt <= 8)
sannsyn = gunstige / N
print(f"Sannsynet for at produktet av to terningar er 8 eller mindre er {round(sannsyn, 3)}")
Sannsynet for at produktet av to terningar er 8 eller mindre er 0.444
Tips
Kodelinja produkt = terning1 * terning2 finn produktet av element på samme plass i dei to arrayene
a = np.array([1, 2, 3, 4, 5])
b = np.array([6, 7, 8, 9, 10])
c = a * b
print(c)
[ 6 14 24 36 50]
Nøyaktighet#
Sjekkar kva som skjer når me triller fleire og fleire terningar. For å visa samanhengen plottar me resultatet. I dømet ser me på sannsynet for å trilla 4 på ein terning.
import matplotlib.pyplot as plt
# antall kast
N = 10000000
# triller terningar
terningar = rng.integers(1, 7, size=N)
# finn den kumulative summen av terningar som er lik 4
kumulativ_sum = np.cumsum(terningar == 4)
# lager "x-akse" frå 1 til N
x = np.arange(1, N + 1)
# finn relativ frekvens
rel_frekvens = kumulativ_sum / x
plt.figure(figsize=(10, 5)) # lagar ein figur med 10x5 mål
plt.hlines(1/6, 0, N, color="red") # teiknar ein linje med farge "red" for den teoretiske verdien
plt.plot(x, rel_frekvens) # plottar x-akse og y-akse
plt.xscale("log") # logaritmisk x-akse
plt.xlabel("Antall kast \n merk: log. skala") # namn på x-aksen
plt.ylabel("Relativ frekvens") # namn på y-aksen
plt.title("Relativ frekvens for terningar") # tittel på figur
plt.show()
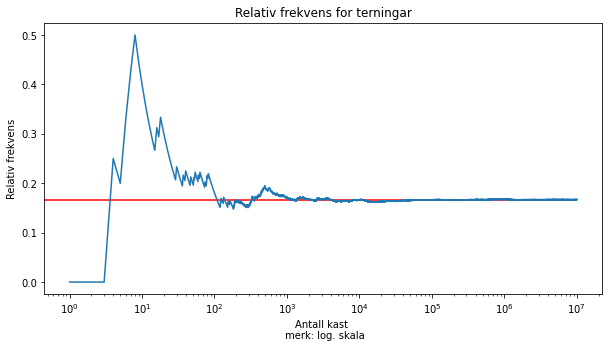
Her ser me at di fleire kast me gjennomfører, di nærare kjem den relative frekvensen den teoretiske verdien for å trilla ein firar på vanleg terning.

