8  Plotting

8.1 Funksjonar med delt forskrift

Nokre funksjonar kan ha ulik definisjon på ulike intervall. Desse kallar me funksjonar med delt forskrift. Me ser på funksjonen

\[f(x) = \begin{cases} x^2 & \text{for } x \leq 0 \\ x & \text{for } x > 0 \end{cases}\]

Denne kan definerast med numpy.piecewise().

import numpy as np
import matplotlib.pyplot as plt

Startar med å definera funksjonen. Det gjer me med

numpy.piecewise(x, condlist, funclist)

der condlist er ei liste med betingelse/intervall og funclist funksjonane i same rekkefølge

def f(x):
    return np.piecewise(x, [x <= 0, x > 0], [lambda x: x**2, lambda x: x])

Kva er lambda?

lambda x: er kortversjonen av

def g(x):
    return x**2

Dermed kan me heller definera funksjonen slik:

x = np.linspace(-3,2,5)
g = lambda x: x**2

y = g(x)

Lagar ein array med 100 \(x\)-verdiar og finn vidare \(y\)-verdiane med funksjonen me definerte.

x = np.linspace(-4,4,100)
y = f(x)

Plottar grafen:

plt.plot(x, y)

# pynt
plt.axhline(0, color="black")
plt.axvline(0, color="black")
plt.grid()
plt.show()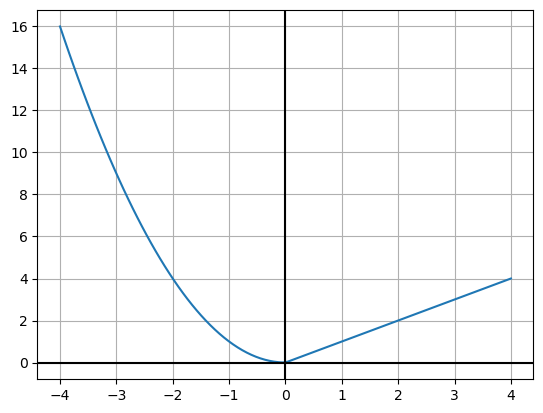

8.1.1 Alternativ: if/else

Ein annan måte dette kan gjerast på er å bruka betingelsar og løkker. Dette kan me gjera slik:

# definerer funksjonen
def f(x):
    if x <= 0:
        return x**2
    else:
        return x

# lager x-verdiar
x_verdiar = np.linspace(-5, 5, 100)

# rekner ut y-verdiane
y_verdiar = [f(x) for x in x_verdiar]

# plottar
plt.plot(x_verdiar, y_verdiar)

# pynt
plt.axhline(0, color="black")
plt.axvline(0, color="black")
plt.grid()
plt.show()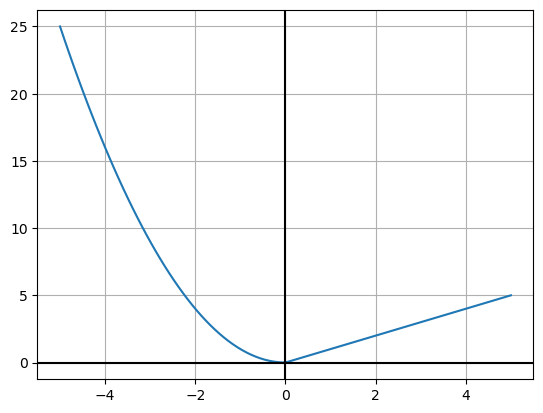

8.1.2 Diskontinuerlege funksjonar

Framgangsmåten over med piecewise kan brukast for funksjonar som er definert for alle \(x\)-verdiar mellom nederste og øverste del av definisjonsmengda. Om ein har ein funksjon med delt definisjonsmengde som td.

\[h(x) = \begin{cases} x^2 & \text{for } x \leq 0 \\ -x^2 & \text{for } x \geq 2 \end{cases}\]

må ein gjera tilpassingar. Prøver først måten me gjorde det over:

# definerer funksjonen
def h(x):
    return np.piecewise(x, [x <= 0, x >= 2], [lambda x: x**2, lambda x: -x**2])


# finn x og y
x = np.linspace(-4, 4, 100)
y = h(x)

# plottar
plt.plot(x, y)
plt.show()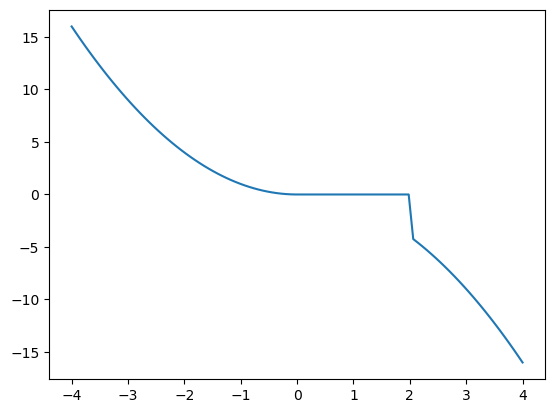

Her viser utfordringa med denne typen funksjonar. I staden for å teikna to kurver som ikkje heng saman, vert funksjonsverdien \(0\) når \(x\in \langle 0, 2 \rangle\). I piecewise sin dokumentasjon finn me dette:

The output is the same shape and type as x and is found by calling the functions in funclist on the appropriate portions of x, as defined by the boolean arrays in condlist. Portions not covered by any condition have a default value of 0.

Måten å løysa det på er å definera kva som skal skje i intervallet der funksjonen ikkje er definert:

# definerer funksjonen (også mellom 0 og 2)
def h(x):
    return np.piecewise(x, [x <= 0, (x > 0) & (x < 2), x >= 2], [lambda x: x**2, np.nan, lambda x: -x**2])


# finn x og y
x = np.linspace(-4, 4, 100)
y = h(x)

# plottar
plt.plot(x, y)
plt.show()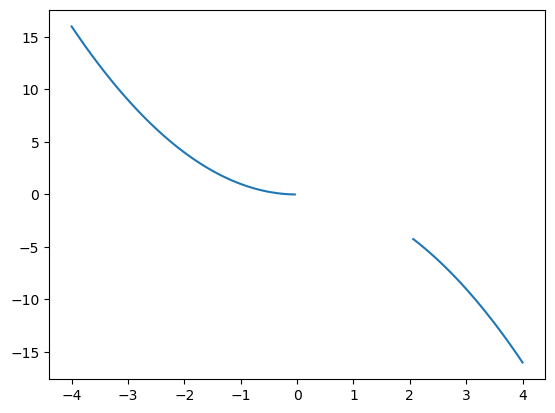

Her er intervallet (x > 0) & (x < 2) definert ved funksjonen np.nan (not a number). På denne måten unngår me at funksjonsverdien vert sett til 0 automatisk i mellomrommet mellom dei to intervalla som utgjer definisjonsmengda.