Hydrologiprogrammering

modellering
programmering
tips
geofag
Forfattar

Torodd F. Ottestad

Publisert

February 2, 2023

📷 Dettifoss, Island

Hydrologiprosjekt i Geofag 1

Her kjem eit døme på korleis ein kan bruka og behandla nokre av dei store hydrologi-datamengdene me har tilgjengeleg i Noreg. Datamaterialet er samla inn av NVE og henta frå Sildre.

📌 I det følgjande dømet nyttar eg vassføringsdata frå Reinsnosvatn

Målestasjonen ligger i Ullensvang i Vestland og er aktiv. Den har vært i drift siden juni 1917 og leverer i dag 3 forskjellige målinger. (sildre.nve.no)

Prosjektet tek altså utgangspunkt i daglege målingar frå 1917!

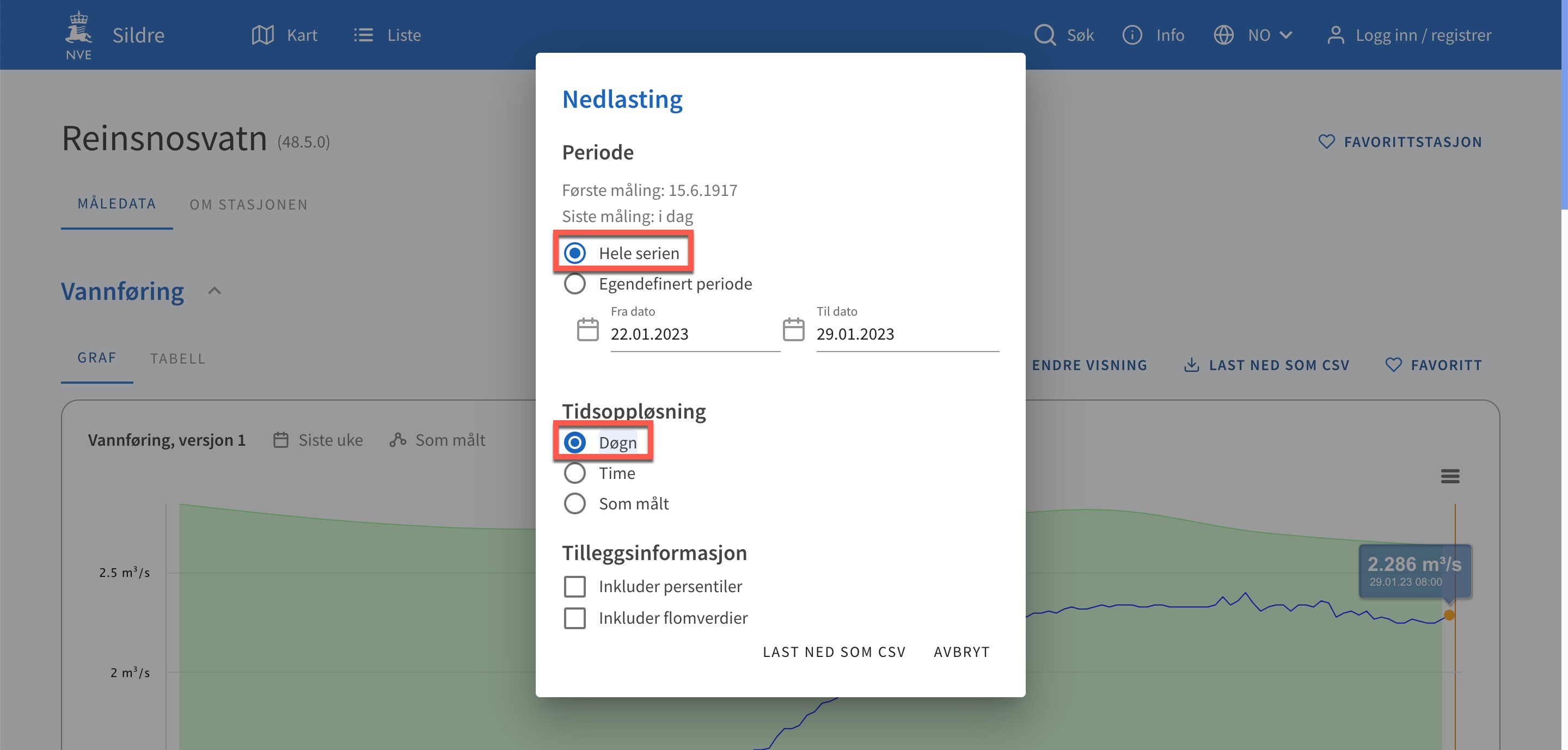
1️⃣ Finn deg ei elv på sildre.nve.no
2️⃣ Trykk på last ned som csv
3️⃣ Kryss av på aktuelle instillingar
4️⃣ Last ned

⬇️ Laste ned data

Importere bibliotek

Vassføringsdataa er lasta ned i csv-format. Me bruker pandas for å jobba med dette effektivt. I tillegg vert det litt plotting og matematikk, så me treng pyplot og numpy i tillegg.

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

Opprette dataramme

CSV-fila med vassføringsdata les me inn i ei dataramme (dataframe). Viss ein tar ein kikk på fila ser ein at det er brukt semikolon for å skilja verdiane, det er to rader før verdiane kjem. Me lagar litt forenkla namn på kolonnene, og les inn data. I tillegg er det nytta komma (og ikkje punktum) som desimalteikn.

🔍 Dei første linjene
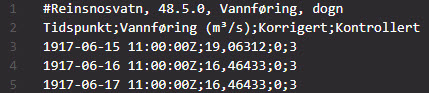
df = pd.read_csv(
    "vassforing_reinsnos_dogn.csv", 
    sep = ";", 
    skiprows = 2, 
    names = ["dato", "Vassføring", "Korrigert", "Kontrollert"], 
    parse_dates = True, 
    decimal=","
)

df.index = pd.to_datetime(df['dato']) 
df.index = pd.to_datetime(df.index.date)
df = df.drop(columns = ["dato", "Korrigert", "Kontrollert"])

Sjekkar dei nyaste fem målingane i tabellen for å sjå at alt ser ok ut.

df.tail()
Vassføring
2023-01-24 1.299365
2023-01-25 1.593457
2023-01-26 2.128418
2023-01-27 2.322153
2023-01-28 2.324195

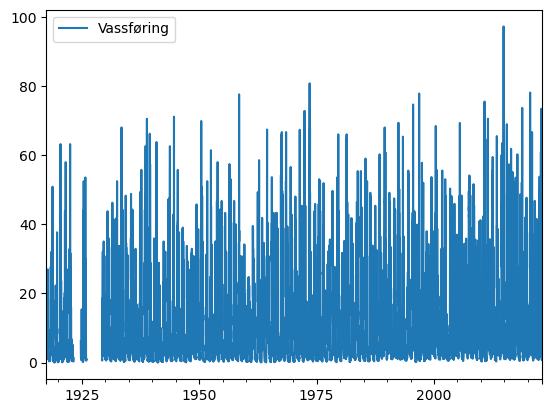
I tillegg kan me prøva å plotta verdiane i dataramma.
Har med ; for å unngå å visa meldinga <AxesSubplot: >

df.plot();

Me ser her at dette ikkje er spesielt nyttig eller informativt, men grafen viser oss at det på 1920-talet er eit par år utan målingar. Korleis dette kan fiksast kjem me attende til litt seinare.

Middelflom

Middelflommen til ei elv er rekna ut frå den største døgnvassføringa per år over eit lengre tidsrom. Frå NVE/varsom.no finn me denne definisjonen:

En middelflom (normal flom) defineres som gjennomsnittet av høyeste vannføring hvert år i en lang årrekke.

For å rekna ut dette må me altså først finna den maksimale vassføringa per år. Bruker groupby i Pandas for å finne dette.

årleg_vf_maks = df.groupby(by=[df.index.year]).max()
årleg_vf_maks.head()
Vassføring
1917 26.98031
1918 50.93218
1919 37.72713
1920 63.26006
1921 58.04514

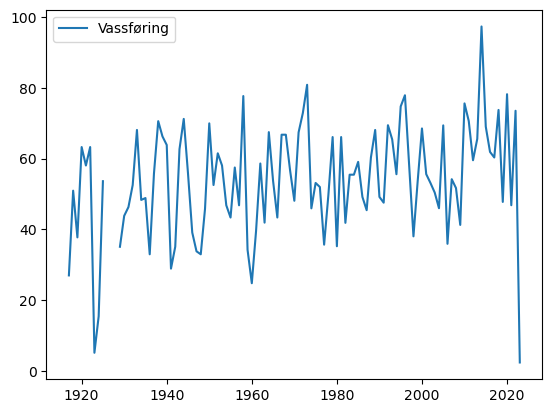
Plottar den nye dataramma årleg_maks som kun har ei måling per år:

årleg_vf_maks.plot();

På grunn av “holet” i målingane tar me berre med data frå 1930 eller seinare med oss vidare. I tillegg er det vinter (og snø/is) for dataa me har for 2023, så me avgrensar til 2022.

årleg_vf_maks = årleg_vf_maks.loc[1930:2022]
årleg_vf_maks.head()
Vassføring
1930 43.82251
1931 46.29647
1932 52.52979
1933 68.09634
1934 48.32775

Me vil finna gjennomsnittleg største årlege vassføring over fleire år. Vel her å sjå på eit gjennomsnitt på 30 år om gongen. Bruker funksjonen rolling og mean i kombinasjon. rolling gjer at me kan gå gjennom dataramma og sjå på dei 30 tidlegare verdiane til kvar rad i tabellen og finna gjennomsnittet (mean) i dette rullande vinduet.

maksvf_og_middelflom = årleg_vf_maks.copy()
maksvf_og_middelflom["Middelflom"] = årleg_vf_maks.rolling(window = 30).mean()

Ser på dei første 5 radene

maksvf_og_middelflom.head()
Vassføring Middelflom
1930 43.82251 NaN
1931 46.29647 NaN
1932 52.52979 NaN
1933 68.09634 NaN
1934 48.32775 NaN

Ser at dei fem første radene i den nye dataramma er NaN (not a number). Dette skjer fordi ein ikkje kan ta gjennomsnitt av dei siste 30 åra før det har gått 30 år… Sjekkar dei nyaste radene i staden:

maksvf_og_middelflom.tail()
Vassføring Middelflom
2018 73.75180 60.571163
2019 47.75206 59.893282
2020 78.19958 60.860965
2021 46.81937 60.837067
2022 73.51824 60.972971

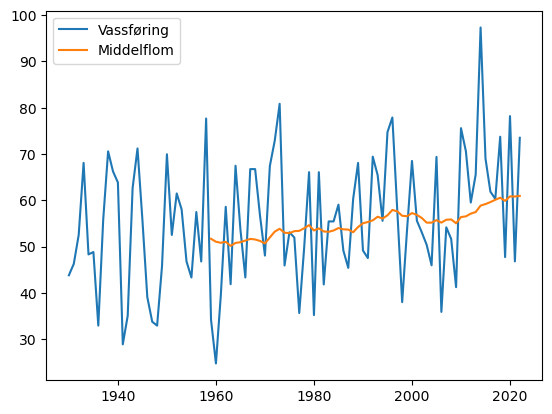
Plottar dataramma og ser korleis dei nye verdiane ser ut:

maksvf_og_middelflom.plot();

Modellering av middelflom

Ser at trenden er oppadgåande og relativt lineær. Ønsker å laga ein lineær modell. Bruker polyfit frå NumPy.

# åra me har data på middelflom
# frå og med 1959 til men ikkje med 2023
x = np.arange(1959, 2023) 

# finn koeffesientane til førstegradspolynomet
a, b = np.polyfit(x, maksvf_og_middelflom["Middelflom"].loc[1959:2022], 1)

# definerer lineær funksjon
def f(x):
    return a*x + b

# plottar dataramma
maksvf_og_middelflom.plot(
    figsize = (20,9), 
    grid = True, 
    fontsize = 16, 
    linewidth = 3, 
    color = ["lightsteelblue", "royalblue"]
)

# plottar modellen
plt.plot(
    x, f(x), 
    linewidth = 2, 
    label = "Modell for middelflom", 
    color = "red"
)

# pynting av plot
plt.title("Vassføring og middelflom\n", fontsize = 24)
plt.legend(fontsize = 16)
plt.ylabel("Vassføring, kubikkmeter/s", fontsize = 16)
plt.xlabel("År", fontsize = 16)
#plt.savefig("Reinsnos - årleg maksvassføring og middelflom.png", dpi = 300)
plt.show()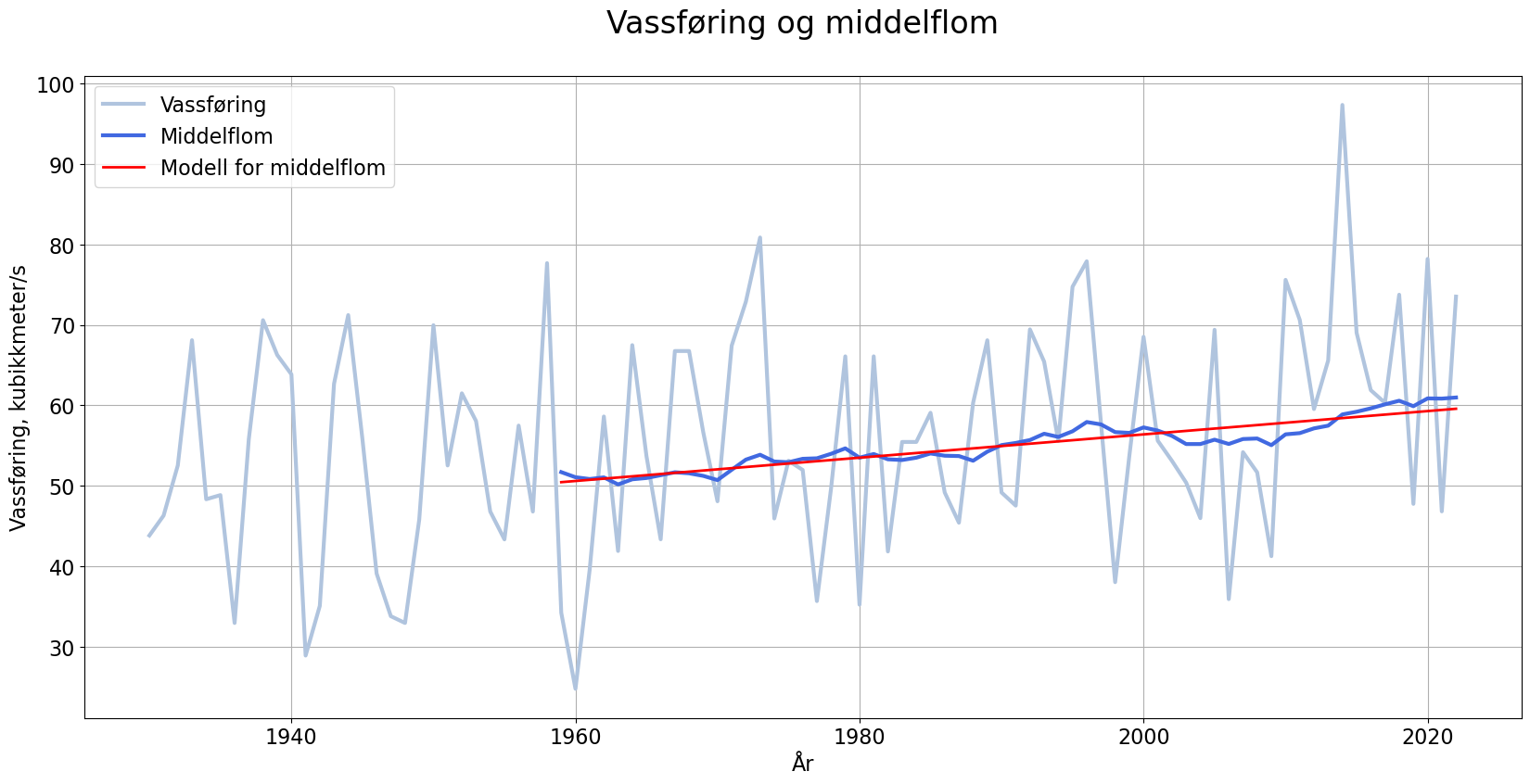

Ekstrapolasjon - modell for framtidig middelflom

Me kan bruka trendlinja for middelflommen som modell for å seie noko om korleis utviklinga vil vera i åra framover (om utviklinga held fram som no):

Kode 
maksvf_og_middelflom.plot(figsize = (20,9), 
                grid = True, 
                fontsize = 16, 
                linewidth = 3, 
                color = ["lightsteelblue", "royalblue"]
               )

plt.plot(x, f(x), 
         linewidth = 1.5, 
         label = "Modell - middelflom", 
         color = "crimson"
        )

# Plottar forlenginga av den lineære modellen
x2 = np.arange(2022, 2101)
plt.plot(x2, f(x2), ":", linewidth = 3, color = "crimson")

# pynting av plot
plt.title("Vassføring og middelflom - modell fram mot 2100 \n", fontsize = 24)
plt.legend(fontsize = 16)
plt.ylabel("Vassføring, kubikkmeter/s", fontsize = 16)
plt.xlabel("År", fontsize = 16)
#plt.savefig("Reinsnos - modellering av middelflom 2100.png", dpi = 300)
plt.show()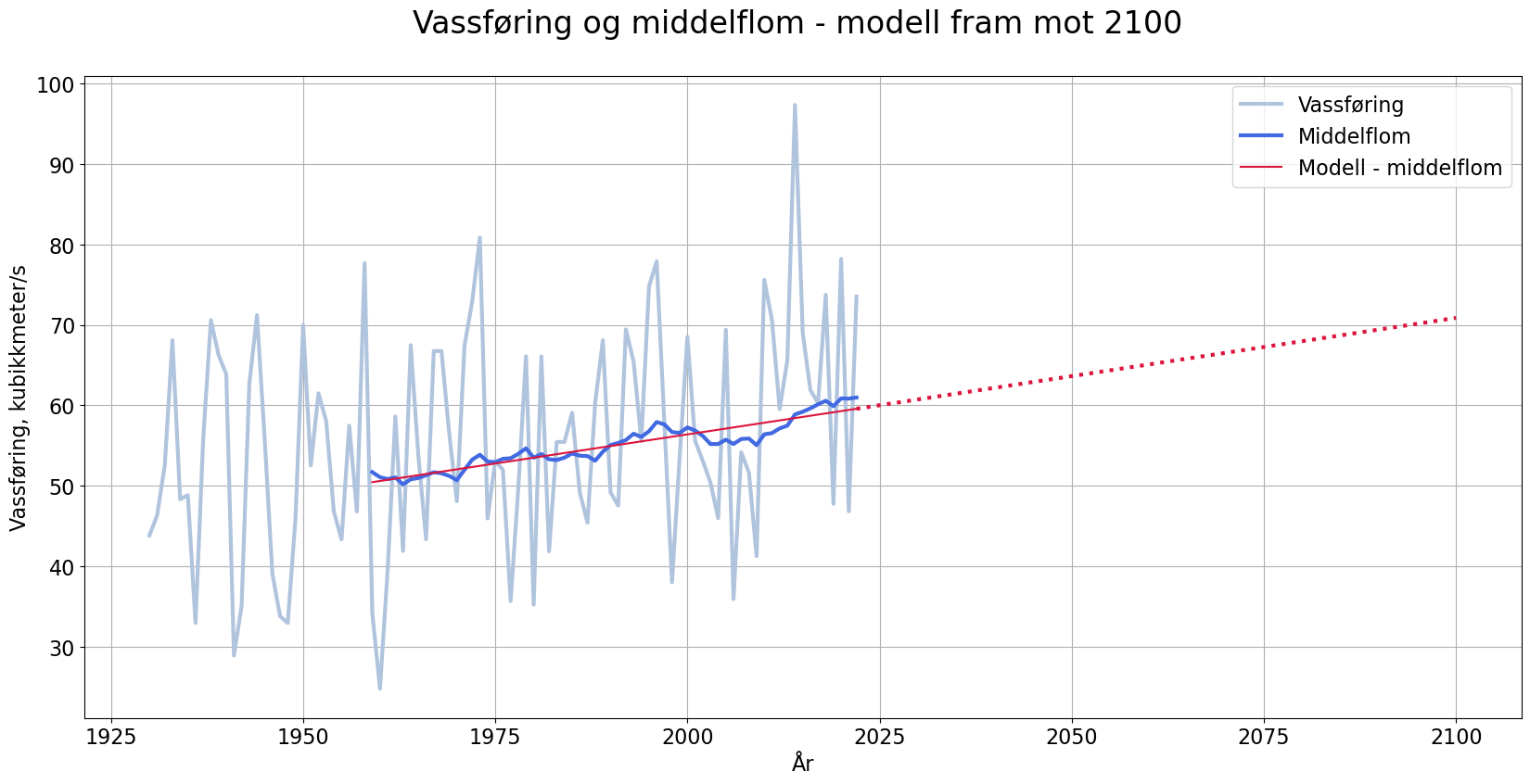

Sjekkar opp mot NVE sine flom-data

Frå stasjonsssida til Reinsnosvatn kan me finna data om ulike typar flom.

Flomdata frå NVE

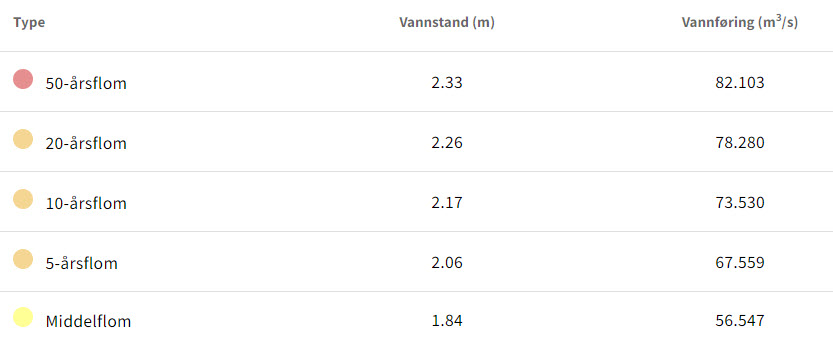
Ser at verdien for 20-årsflom er 78,28 \(m^3/s\). Plottar inn linja \(y=78,28\) i samme figur som tidlegare. Bruker plt.axhline() for å teikna horisontal linje.

Kode 
# åra me har data på middelflom
# frå og med 1959 til men ikkje med 2023
x = np.arange(1959, 2023) 

# finn koeffesientane til førstegradspolynomet
a, b = np.polyfit(x, maksvf_og_middelflom["Middelflom"].loc[1959:2022], 1)

# definerer lineær funksjon
def f(x):
    return a*x + b

# plottar dataramma
maksvf_og_middelflom.plot(
    figsize = (20,9), 
    grid = True, 
    fontsize = 16, 
    linewidth = 3, 
    color = ["lightsteelblue", "royalblue"]
)

# plottar modellen
plt.plot(
    x, f(x), 
    linewidth = 2, 
    label = "Modell for middelflom", 
    color = "red"
)

# plottar 20-årsflom
plt.axhline(
        y = 78.28,
        color = "crimson", 
        linewidth = 3, 
        linestyle = ":", 
        label = "20-årsflom"
)

# pynting av plot
plt.title("Vassføring og middelflom\n", fontsize = 24)
plt.legend(fontsize = 16)
plt.ylabel("Vassføring, kubikkmeter/s", fontsize = 16)
plt.xlabel("År", fontsize = 16)
#plt.savefig("Reinsnos - årleg maksvassføring og middelflom.png", dpi = 300)
plt.show()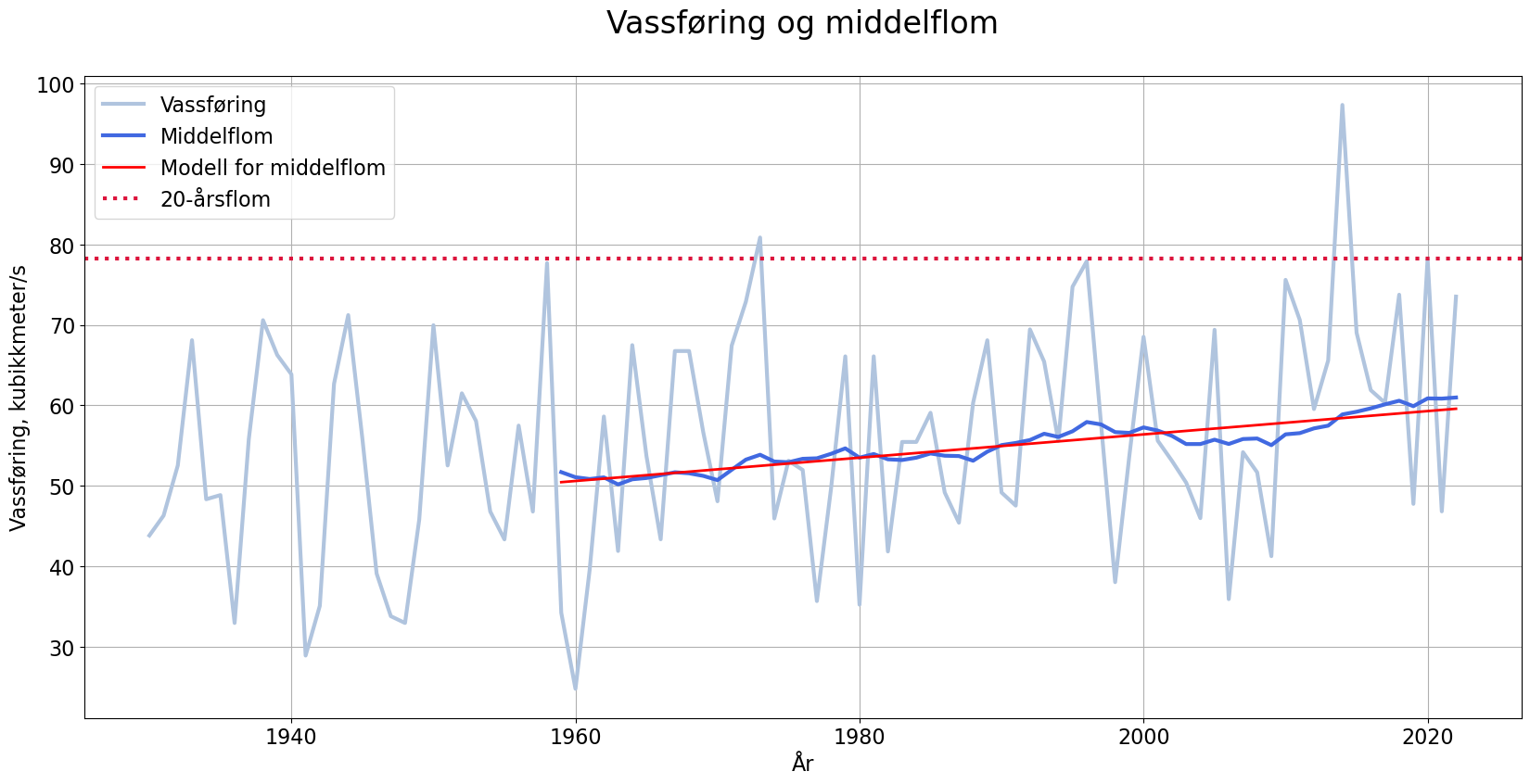

Tips til oppgåver

Plott linjer for dei ulike flom-typane. Kor godt stemmer observasjonane med desse tala?
Kva ligg i omgrepet 20-årsflom?

Hydrogram - vassføring per dag

Denne store tabellen vår med daglege data frå over 100 år kan me gjera mykje gøy med. Me kan t.d. sortera alle observasjonane til dag i året, og sjå korleis vassføringa vanlegvis er gjennom eit år. I koden under gjer me dette, og i tillegg fargelegg me området mellom 25 og 75-persenilen. På denne måten får me fargelagt dei 50% midterste målingane per dag. Det er òg greitt å visa medianen (som blir hydrogrammet) på figuren.

Startar med å sortera den opprinnelege df til dag i året (day of year - doy). Etterpå grupperer me materialet i ein ny tabell.

df['doy'] = df.index.dayofyear
df['år'] = df.index.year
df.head()
Vassføring doy år
1917-06-15 19.06312 166 1917
1917-06-16 16.46433 167 1917
1917-06-17 16.46433 168 1917
1917-06-18 18.67722 169 1917
1917-06-19 21.97948 170 1917

Lagar ein pivottabell med dag i året som rader og årstal som kolonner

piv = pd.pivot_table(df, index=['doy'],columns=['år'], values=['Vassføring'])
piv.head()
Vassføring
år 1917 1918 1919 1920 1921 1922 1923 1924 1925 1929 ... 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023
doy
1 NaN 0.751369 0.520992 0.110245 0.520992 2.268141 0.858653 NaN 4.303123 NaN ... 4.858096 1.869427 4.191920 28.483190 4.161459 2.347107 12.096400 2.466642 4.124214 2.000038
2 NaN 0.751369 0.481094 0.095431 0.562897 2.268141 0.751369 NaN 4.003652 NaN ... 4.406689 3.295648 3.810454 19.011320 3.759124 2.669421 8.641389 2.288357 5.344579 1.913351
3 NaN 0.701046 0.443164 0.095431 0.606849 2.166990 0.803893 NaN 3.858951 NaN ... 3.952404 4.470398 3.068896 11.995200 3.438255 2.515568 8.580434 2.122319 6.083396 1.827513
4 NaN 0.701046 0.407161 0.095431 0.652886 1.973261 0.915689 NaN 3.717565 NaN ... 3.694488 4.407481 2.748646 8.526679 3.053644 2.336836 7.108252 1.954245 5.640584 1.779285
5 NaN 0.652886 0.373045 0.110245 0.803893 1.703600 0.915689 NaN 3.444615 NaN ... 3.422920 4.161712 2.613774 6.329734 2.739008 2.265773 5.907576 1.806864 4.668677 1.701279

5 rows × 104 columns

Utrekningar

Finn ulike verdiar per dag i året over dei 104 åra.

piv["min"] = piv.min(axis = 1)
piv["maks"] = piv.max(axis = 1)
piv["75%"] = piv.quantile(q = 0.75,axis = 1)
piv["median"] = piv.median(axis = 1)
piv["25%"] = piv.quantile(q = 0.25,axis = 1)

piv.head()
Vassføring min maks 75% median 25%
år 1917 1918 1919 1920 1921 1922 1923 1924 1925 1929 ... 2019 2020 2021 2022 2023
doy
1 NaN 0.751369 0.520992 0.110245 0.520992 2.268141 0.858653 NaN 4.303123 NaN ... 2.347107 12.096400 2.466642 4.124214 2.000038 0.110245 28.48319 2.589138 1.381706 0.701046
2 NaN 0.751369 0.481094 0.095431 0.562897 2.268141 0.751369 NaN 4.003652 NaN ... 2.669421 8.641389 2.288357 5.344579 1.913351 0.095431 19.01132 2.548025 1.417153 0.652886
3 NaN 0.701046 0.443164 0.095431 0.606849 2.166990 0.803893 NaN 3.858951 NaN ... 2.515568 8.580434 2.122319 6.083396 1.827513 0.095431 11.99520 2.491543 1.381060 0.606849
4 NaN 0.701046 0.407161 0.095431 0.652886 1.973261 0.915689 NaN 3.717565 NaN ... 2.336836 7.108252 1.954245 5.640584 1.779285 0.095431 14.41007 2.421806 1.275205 0.652886
5 NaN 0.652886 0.373045 0.110245 0.803893 1.703600 0.915689 NaN 3.444615 NaN ... 2.265773 5.907576 1.806864 4.668677 1.701279 0.110245 18.95604 2.372195 1.207931 0.728653

5 rows × 109 columns

Plottar

# Plottar minimumsverdiar
piv["min"].plot(
    figsize = (20, 8),
    color = "seagreen", 
    linewidth = 0.8, 
    grid = False, 
    fontsize = 18, 
    legend = False,
    label = "Minste verdi"
)

# PLottar maksimumsverdiar
piv["maks"].plot(
    color = "seagreen", 
    linewidth = 0.8, 
    grid = False, 
    fontsize = 18, 
    legend = False,
    label = "Største verdi"
)

# Fargelegg området mellom 25- og 75-persentilane
plt.fill_between(
    piv.index, 
    piv["25%"], piv["75%"], 
    facecolor='green', 
    alpha=0.2, 
    interpolate=True,
    label = "25% - 75%"
)

# Plottar medianen
piv["median"].plot(
    linewidth = 2, 
    color = "darkgreen",
    label = "Median"
)

# Pyntar på plottet
plt.xlabel("Dag i året \n (01. jan - 31. des)", fontsize = 18)
plt.ylabel("Vassføring i $m^3/s$", fontsize = 18)
plt.title("Vassføring - per dag i året \n", fontsize = 24)
plt.legend(fontsize = 16)
plt.savefig("Reinsnos - vassføring per dag gjennom året.png", dpi = 300)
plt.show()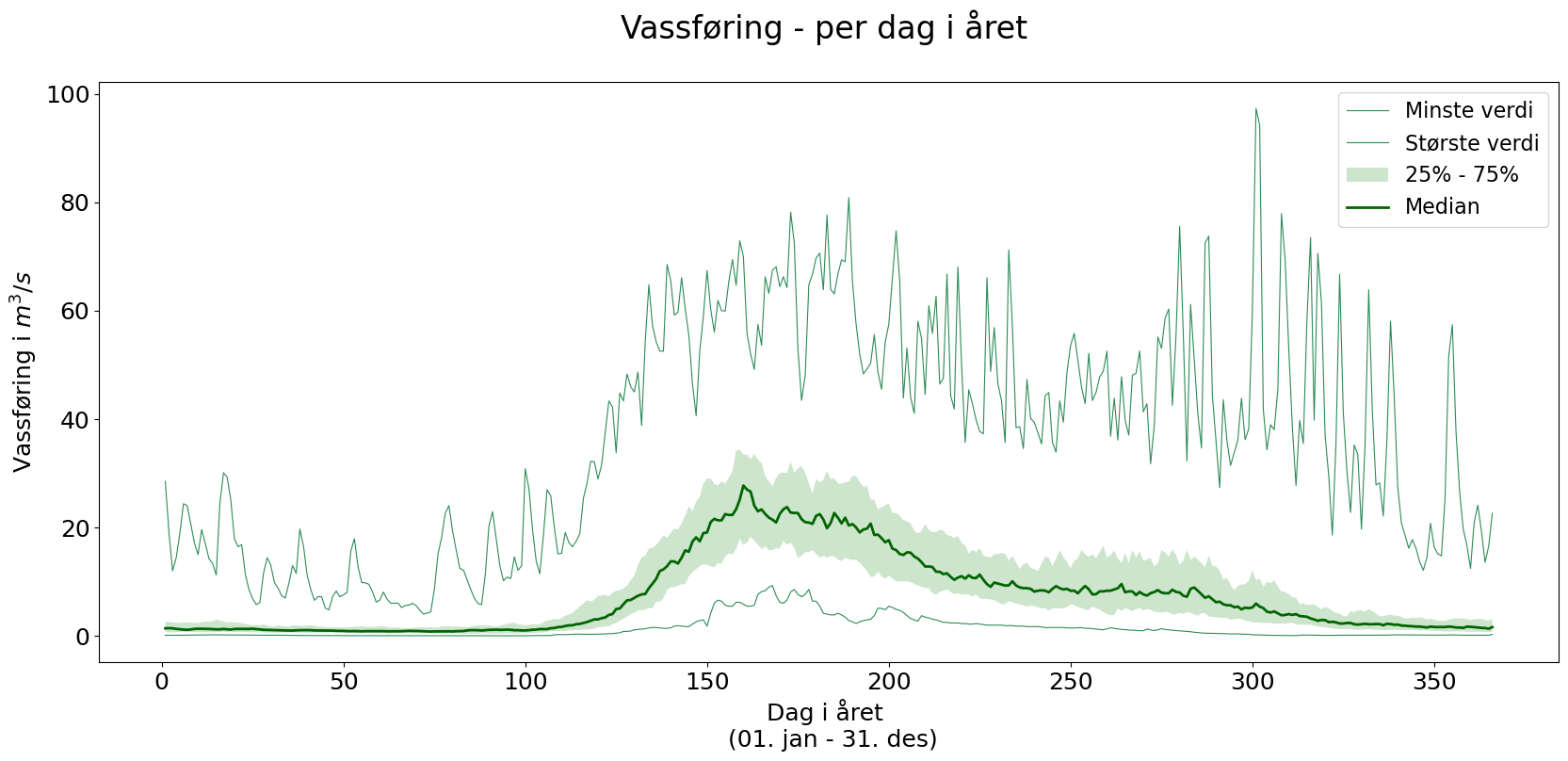

Oppsummert

Det er mykje kjekt ein kan gjera med vassføringsdata frå NVE. Både det å laga plott som me har gjort over, og arbeida med store datamengder som dette kan erfaringsmessig gje elevane god innsikt i samanhengar og forståing for omgrep i hydrologien.

Tips til undervisinga

Dei elevlaga hydrogramma er eit godt utganspunkt for diskusjonar og utforsking.

1️⃣ Jobb med koden saman med elevane. Lag plotta.
2️⃣ Be elevane om å finna andre elver (ulik storleik, ulik geografisk plassering) og lage eigne plott.
3️⃣ Sjå på ulike hydrogram laga av elevane (utan namn på vassdraget) og ha diskusjon i klassen om kva informasjon som ligg i plotta (Nord/sør/aust/vest? Høgde? Isbre? Snøsmelting/regnflom? Regulering?)
4️⃣ Avslør namn og plassering - korleis stemte det?

Gjenbruk